えっ・・・これ覚えんの・・・?
全て出るわけではもちろんありませんが,やっぱりある程度出ます。
出来るだけ覚えた方がよいですが、まず赤字のやつはすぐにだせるようにしてください(筆者の主観的な部分もありますのであくまでも参考に)。
|
波長(λ) 生体内の音速(c) 周波数(f) の関係式 $$c=f×λ$$ $$ λ=\frac{c}{f}$$ *Hz・・・1秒間あたりの波の揺れる回数(周波数)を表す単位 |
問題1 |
|
距離分解能(Δx) $$\Delta x=\frac{n\lambda}{2}$$ |
問題2 |
|
周波数(F) 「1秒間に何回振動するか」 T=周期(sec)
$$F=\frac{1}{T}[Hz]$$ |
問題3 |
|
音の伝播速度 κ:媒質の弾性率 ρ:媒質の密度 $$c=\sqrt{\frac{κ}{ρ}}$$ |
|
|
音圧(pressure) $$dB=20 \log(P2:変化後)/(P1:変化前)$$ |
|
|
強度(intensity) $$dB=10 \log(I2:変化後)/(I1:変化前)$$ |
|
|
振幅(amplitude) $$dB=20 \log(A2:変化後)/(A1:変化前)$$ |
|
|
音響パワー(power) $$dB=10 \log(P2:変化後)/(P1:変化前)$$ |
|
|
音響インピーダンス:Z ρ=媒質の密度 c=媒質固有の媒質中の音速 $$反射強度R_{i}$$ $$透過強度T_{i}=1-R_{i}$$
Z=ρ×c $$R_{i}=\left( \frac{Z_{2}-Z_{1}}{Z_{2}+Z_{1}} \right)^2 (垂直入射時)$$ $$ 透過強度T_{i}=1-R_{i}=\frac{4×Z_{2}Z_{1}}{\left(Z_{2}+Z_{1}\right)^2}$$
$$R_{i}=\left( \frac{Z_{2}\cos θ_{1}-Z_{1}\cos θ_{2}}{Z_{2}\cos θ_{1}+Z_{1}\cos θ_{2}} \right)^2$$ $$θ_{1}=入射角=反射角,θ_{2}=屈折角$$ |
問題4 |
|
スネルの法則 $$\frac{\sin θ_{1}}{c_{1}}=\frac{\sin θ_{2}}{c_{2}}$$ |
|
|
Qファクター(周波数の分布の状態を表すもの) *強さが最大値の$$\frac{1}{\sqrt{2}}\fallingdotseq-3[dB]$$となるところを帯域幅とするのが一般的
$$Q=\frac{F_{0}}{\Delta F}$$ *帯域幅(ΔF)が広いほどQ値は小さくなり, ΔFが狭いほどQ値は高くなる
$$比帯域=\frac{1}{Q}$$ |
|
|
ナイキスト周波数=最大検出ドプラ周波数 $$検出可能なドプラ偏移の範囲F_{dMAX}$$ PRF:パルス繰り返し周波数
$$F_{dMAX}=\pm \frac{PRF}{2}$$ |
|
|
音が生体内をc=1530[m/sec]で一定に進むとすると,音が生体内で1cm進んで反射して返ってくる時間 音が生体内で1cm進んで反射して返ってくる時間=13μs(←数値を覚えとくと便利) |
問題6 |
|
PRF[Hz]:パルス繰り返し周波数
$$PRF=\frac{1}{繰り返し周期}[Hz]$$ |
問題7 |
|
走査線数:N[本] 音速:c(1530[m/sec]) 視野深度:D[cm] 1秒間に描出できる画像の数(フレーム数):R(枚) (1枚の画像を描出する時にかかる時間:T)$$ T=N×\frac{2D}{c}$$ $$R=\frac{1}{T}$$
$$R×D×N=\frac{c}{2}$$ |
問題8 |
|
パルスドップラーの最大検出可能速度に関しての公式たち Fo=送信周波数 Fd=ドプラ偏位 D=視野深度 PRF=パルス繰り返し周波数 $$V_{MAX}=\pm\frac{c^{2}}{8\cos θ×F_{0}×D}$$ $$V=\frac{c}{2×\cos θ}×\frac{Fd}{Fo}$$ $$Fd=\frac{2×V×\cosθ}{C}×F_{0}$$ $$FdMAX=\pm\frac{PRF}{2}$$
$$V_{MAX}=\pm \frac{c×PRF}{4×\cos θ×F_{0}}$$
$$PRF=\frac{c}{2D}$$ |
|
Q問題1 媒質Aの音速を1500[m/s]とした時,周波数F=10.0[MHz]の波長は?
解答.公式は簡単ですがポイントは「単位」です。実際の試験でも混乱しないように類似の問題で練習してください。
$$ λ=\frac{c}{f}$$
$$\lambda=\frac{1500[m/sec]}{10.0[MHz]}$$
$$=\frac{1.5×10^{6} [mm/sec]}{10.0×10^{6}[Hz]}$$
=0.15[mm]
問題2.距離分解能を向上をさせるためには波長,波数がどのような条件であればよいか?
解答.
$$\Delta x(距離分解能)=\frac{n\lambda}{2}$$ $$ λ=\frac{c}{f}$$
距離分解能を向上させるのは、上式より,
・波長λが一定の時、波数nをを少なく
問題3. 周期=10[msec]おきに振動が繰り返されている場合の周波数は?
解答.$$F=\frac{1}{10[msec]}[Hz]$$
$$=\frac{1}{0.01[sec]}[Hz]=100[Hz]$$
問題4
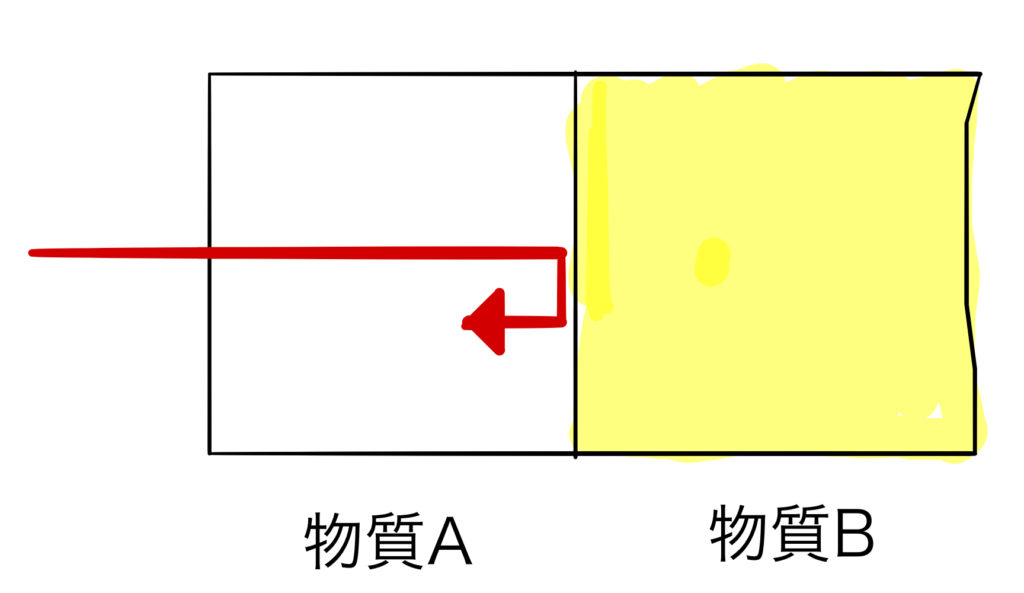
$$A:\rho=1.0×10_{3}[kg/m_{3}],c=1500[m/sec] $$
$$B:\rho=3.0×10_{3}[kg/m_{3}],c=1000[m/sec]$$
物質A,Bの音響インピーダンスは? 物質Aから物質Bに対して垂直に入射した時の反射強度は?
解答
$$Z_{A}=\rho×c=1.0×10^{3}[kg/m^{3}]×1500[m/sec]$$
$$=1.5×10^{6}[kg/m^{2}・sec]$$
$$Z_{B}=\rho×c=3.0×10^{3}[kg/m^{3}]×1000[m/sec]$$
$$=4.5×10^{6}[kg/m^{2}・sec]$$
$$R_{i}=\left( \frac{Z_{2}-Z_{1}}{Z_{2}+Z_{1}} \right)^2$$
$$R_{A→B}=\left( \frac{Z_{B}-Z_{A}}{Z_{B}+Z_{A}} \right)^2$$
$$=\left( \frac{4.5-1.5}{4.5+1.5} \right)^2=\left( \frac{1}{2} \right)^2$$
問題5.
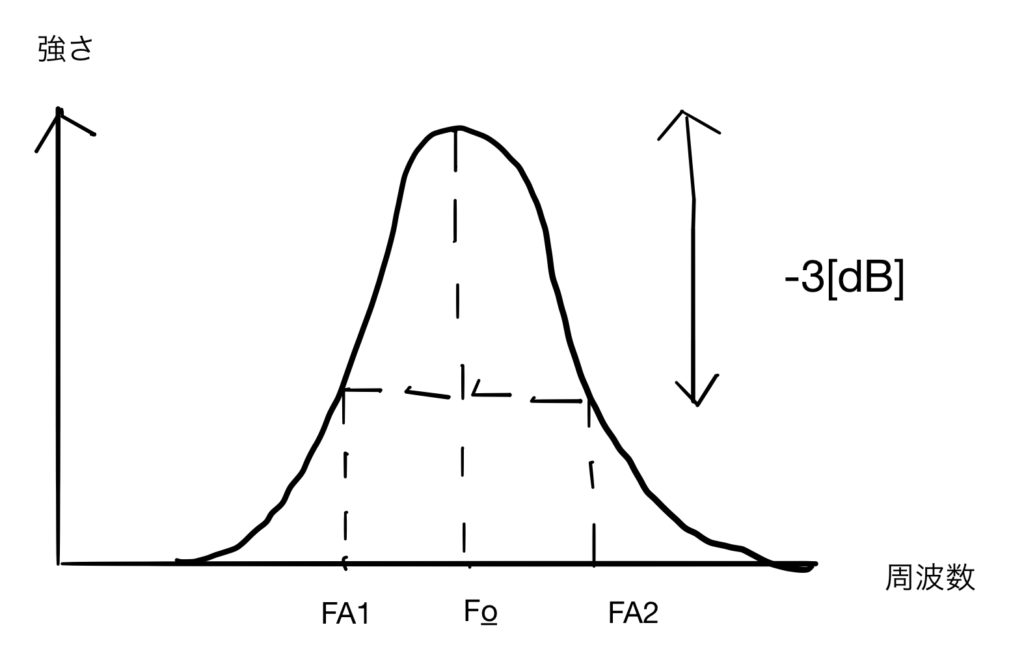
上図において$$F_{0}=5.0[MHz],FA1=4.5[MHz],FA2=5.5[MHz]の時,帯域幅とQファクターと比帯域は?
解答.
帯域幅=1.0{MHz]で,Qファクターは$$Q=\frac{F_{0}}{\Delta F}$$ $$Q=\frac{5.0}{1.0}=5.0$$
問題6.音が生体内をc=1530[m/sec]で一定に進むとすると,音が生体内で1cm進んで反射して返ってくる時間は?
解答.まず音が生体内で1cm進むのにかかる時間を計算すると,
$$ \frac{1[cm]}{1530[m/sec]}=\frac{1×10^{-2}[m]}{1.53×10^{3}[m/sec]}&&
&&\fallingdotseq6.5×10^{-6}[s]=6.5[μs]$$
問題7.PRFが7.5kHzだとするとその繰り返し周期は?また,その視野深度は?(受信から次の送信時間を無視するものとする).
$$繰り返し周期= \frac{1[cm]}{7.5[kHz]}=\frac{1[cm]}{7500[Hz]}&&
&&\fallingdotseq133[μs]$$
生体内を超音波1cmあたりの往復時間は13μsなので、
$$ \frac{133[μs]}{13[μs/cm]}\fallingdotseq10[cm]$$
すなわち10cmの視野深度からの反射エコーを受信できることとなる.
問題8 走査線数N=153本,視野深度がD=10cmとすると、1枚の画像を描出するのにかかる時間Tと1秒間に描出できるフレーム数は?
解答8.
$$T=153×\frac{2×10[cm]}{153×10^{3}[cm/sec]}$$
$$=2×10^{-2}[sec]=20[msec]$$
フレーム数は$$R= \frac{1}{T}= \frac{1[sec]}{20[msec]}=50[枚]$$
問題9血管に対して入射角0度で10MHzの信号を送信して,10.5MHzの反射信号を受信した.この血流速度は?
解答.
$$V=\frac{c}{2×\cos θ}×\frac{Fd}{Fo}$$
$$V=\frac{1530}{2×1}×\frac{0.5}{10}=38.25[m/sec]$$
問題10.$$F_{0}=5{MHz},PRF=12{kHZ}$$
$$c=1530[m/sec],θ=0°とした時,$$
パルスドプラ最大検出速度と最大視野深度は?
解答.
$$V_{MAX}=\pm \frac{c×PRF}{4×\cos θ×F_{0}}$$
$$V_{MAX}=\pm \frac{1530[m/sec]×12[kHz]}{4×1×5000[kHz]}$$
$$\fallingdotseq \pm0.92[m/sec]$$
この時、最大視野深度は$$PRF=\frac{c}{2D} \iff D_{max}=\frac{c}{2×PRF}$$
$$=\frac{1530[m/sec]}{2×12000[Hz]}\fallingdotseq 0.0638[m]=6.4cm $$
*間違いなどありましたら下のコメント欄で指摘して頂ければ幸いです。